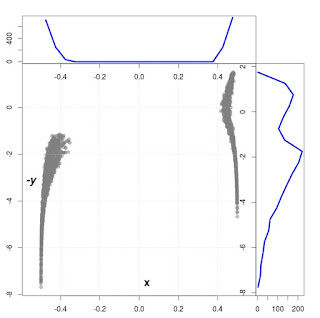
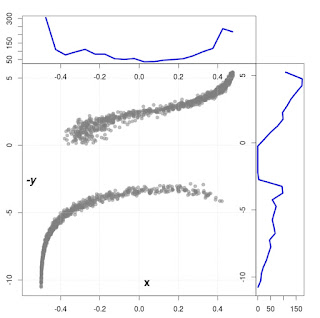
And so, it is a natural choice to use the survival method in forecasting of financial market. Especially, for prediction of future price behaviour of a given financial instance and as a consequence for generating buy-sell signals. Searching for some examples of similar analysis I have found only a single work addressing the subject [1]. From this publication I adopted a definition of a daily revenue - given below.
In this note I would like to show how to use the survival analysis method for generation of buy/sell signals for a chosen financial product. As data I use Brent Oil Future options, however the method could be adopted to other instruments as well.
The analysis is presented in R language.
As an input I use historical data of Brent Oil Future options available on the portal stooq.pl. The data contain several features like Open and Close prices, Volume, highest (High) and lowest (Low) prices and Open Interest (OpenInt). Operating on a daily basis, my goal is to predict whether for the next day we expect increase or decrease of the Close value.
Let me begin with preparation of libraries and data engineering.
set.seed(1)
library(ggplot2)
library(lubridate)
library(readr)
library(MASS)
library(survival)
library(xts)
library(rms)
# reading the data:
myDir <- "/analysis/forecasting/data_stooq.pl/"
myFile <- "sc_f_d_2015_2016.csv"
input <- NULL
input <- read.csv(paste(myDir,myFile,sep=""),header=TRUE)
names(input)
[1] "Date" "Open" "High" "Low"
[5]"Close" "Volume" "OpenInt"
- $corp = Close - Open$ : it corresponds to the definition of the corp of the candlesticks,
input$corp <- 0 input$corp <- input$Close - input$Open - Exponential Moving Average - $EMAV$. For this purpose I use functions for calculation of the
Volume Weighted Exponential Moving Average (see volume-weighted-exponential-moving-average)
VEMA.num <- function(x, volumes, ratio) { ret <- c() s <- 0 for(i in 1:length(x)) { s <- ratio * s + (1-ratio) * x[i] * volumes[i]; ret <- c(ret, s); } ret } VEMA.den <- function(volumes, ratio) { ret <- c() s <- 0 for(i in 1:length(x)) { s <- ratio * s + (1-ratio) * volumes[i]; ret <- c(ret, s); } ret } VEMA <- function(x, volumes, n = 10, wilder = F, ratio = NULL, ...) { x <- try.xts(x, error = as.matrix) if (n < 1 || n > NROW(x)) stop("Invalid 'n'") if (any(nNonNA <- n > colSums(!is.na(x)))) stop("n > number of non-NA values in column(s) ", paste(which(nNonNA),collapse = ", ")) x.na <- xts:::naCheck(x, n) if (missing(n) & !missing(ratio)) { n <- trunc(2/ratio - 1) } if (is.null(ratio)) { if (wilder) ratio <- 1/n else ratio <- 2/(n + 1) } foo <- cbind(x[,1], volumes, VEMA.num(as.numeric(x[,1]), volumes, ratio), VEMA.den(volumes, ratio)) (foo[,3] / foo[,4]) -> ma ma <- reclass(ma, x) if (!is.null(dim(ma))) { colnames(ma) <- paste(colnames(x), "VEMA", n, sep = ".") } return(ma) } x <- ts(input$Close) input$EMAV <- 0 Vol <- rep(1, length(input[,1])) input$EMAV <- VEMA(input$Close, Vol,ratio=0.95) plot(input$Close,type="l");lines(input$EMAV,col="red") - Daily Revenue - $DailyRevenue$ . The feature is calculated as a percentage of $Close$ values between present and previous days [1]
$DailyRevenue = \frac{( Close[k] - Close[k-1] )}{Close[k-1]} \cdot 100$input$DailyRevenue <- 0 input$DailyRevenue[1] <- 0 for (k in (2:(length(input$Close)))) { input$DailyRevenue[k] <- (input$Close[k]-input$Close[k-1])*100/(input$Close[k-1]) } - Censors:
In this case I consider two series of censored data corresponding to the increasing and decreasing values of $DailyRevenue$. The increasing or decreasing event is detected by checking whether the Daily Revenue is larger or smaller than a given threshold value. The threshold value could be used as a parameter in our model. Therefore, the value of the $threshold$ could be different from $0$ ($0$ is here a good initial choice). The censoring of data used in the model is following:- censors specific for increasing daily revenue: $censorUp$:
if the daily revenue is higher than $threshold$: $censorUp = 0$ (censored point of time).
In case when the daily revenue being smaller or equal to $threshold$: $censorUp = 1$ .
Threshold <- 0 input$censorUp <- 0 input[input$DailyRevenue <= Threshold,12] <- 1 - censors specific for decreasing daily revenue: $censorDown$. In this case the
events are opposite to the $censorUp$ feature.
The daily revenue is smaller or equal to $threshold$: $censorDown = 1$ .
the daily revenue is larger than $threshold$: $censorDown = 0$ .
input$censorDown <- 0 input[input$DailyRevenue > Threshold,11] <- 1
- censors specific for increasing daily revenue: $censorUp$:
if the daily revenue is higher than $threshold$: $censorUp = 0$ (censored point of time).
In case when the daily revenue being smaller or equal to $threshold$: $censorUp = 1$ .
- Time to events:
are measured as a time distance between last local extremum of the $DailyRevenue$ and an event defined by censoring series (censored or NOT censored).
- $TimeToEventUp$:
it is a time measured from a last local minimum of the $DailyRevenue$ to the $censorUp = 1$ events or the time distance between the last local maximum of the $DailyRevenue$ to the $censorUp = 0$.locmylastmin <- 1 locmylastmax <- 1 for (k in (2:(dim(input)[1]))) { tmp <- input$DailyRevenue[1:k] if (input$censorUp[k] == 0) { # find all local minima: locmymin <- which(diff(sign(diff(tmp)))==+2)+1 if (length(locmymin) == 0) {locmymin <- which.min(tmp)} locmylastmin <- locmymin[length(locmymin)] dateMin <- input[locmylastmin,1] input$TimeToEventUp[k] <- as.integer(as.Date(input[k,1])- as.Date(dateMin)) } if (input$censorUp[k] == 1) { # find all local maxima: locmymax <- which(diff(sign(diff(tmp)))==-2)+1 if (length(locmymax)==0) {locmymax <- which.max(tmp)} locmylastmax <- locmymax[length(locmymax)] dateMax <- input[locmylastmax,1] input$TimeToEventUp[k] <- as.integer(as.Date(input[k,1])- as.Date(dateMax)) } } - $TimeToEventDown$:
is calculated in an opposite way to the feature $TimeToEventUp$. Details of determination of the $TimeToEventDown$ feature is shown on Fig. 1 .locmylastmin <- 1 locmylastmax <- 1 for (k in (2:(dim(input)[1]))) { tmp <- input$DailyRevenue[1:k] if (input$censorDown[k] == 1) { # find all local minima: locmymin <- which(diff(sign(diff(tmp)))==+2)+1 if (length(locmymin) == 0) {locmymin <- which.min(tmp)} locmylastmin <- locmymin[length(locmymin)] dateMin <- input[locmylastmin,1] input$TimeToEventDown[k] <- as.integer(as.Date(input[k,1])- as.Date(dateMin)) } if (input$censorDown[k] == 0) { # find all local maxima: locmymax <- which(diff(sign(diff(tmp)))==-2)+1 if (length(locmymax)==0) {locmymax <- which.max(tmp)} locmylastmax <- locmymax[length(locmymax)] dateMax <- input[locmylastmax,1] input$TimeToEventDown[k] <- as.integer(as.Date(input[k,1])- as.Date(dateMax)) } }
Definition of the variable $TimeToEventDown$ demonstrated on a part of the $DailyRevenue$ time series.
It is a sequence of time distances $T_{Down}^{censored}$ and $T_{Down}^{event}$, where
the time $T_{Down}^{censored}$ is a time measured from a last local maximum of the $DailyRevenue$ to the $censorDown = 0$ and
$T_{Down}^{event}$ - is the time distance between the last local $DailyRevenue$ minimum to the $censorDown = 1$.
- $TimeToEventUp$:
In the next step I build the signal creator.
The basic part is realized in the standard way of calculating of the survival probabilities corresponding to the both series $censorUp$ and $censorDown$. The prediction is calculated by the function survfit without newdata object. In such a case the predicted survival probabilities are calculated on a base of mean values of all covariates included in the formula used for creation of the Cox hazards regression model fit. In our case I use all available covariates in implemented formula, except the $Volume$ feature which is not already a solid number.
formula = Surv(TimeToEventDown, censorDown) ~
High + Low + Close + corp + EMAV + DailyRevenue + OpenInt
SurvivalProb <- function(myinput,What="Down") {
train <- myinput
if (What == "Down") {
coxphCorp <- coxph(Surv(TimeToEventDown, censorDown) ~
High + Low + Close + corp + EMAV + DailyRevenue + OpenInt,
data=train, method="breslow")
}
if (What == "Up") {
coxphCorp <- coxph(Surv(TimeToEventUp, censorUp) ~
High + Low + Close + corp + EMAV + DailyRevenue + OpenInt,
data=train, method="breslow")
}
mysurffit<-survfit(coxphCorp, se.fit = F, conf.int = F)
tmp<-summary(mysurffit)
myprob <- tmp$surv[1]
myprob
}
The code of the function $SignalPredictor$ :
SignalPredictor <- function(train,ratioValue) {
# Survival-Probability-that-daily-revenue-will-be-smaller-next-day
ProbDown <- SurvivalProb(train,"Down")
# Survival-Probability-that-daily-revenue-will-be-higher-next-day
ProbUp <- SurvivalProb(train,"Up")
# signal: + <- buy; - <- sell
signal <- ((ProbUp/ProbDown)-ratioValue)
signal
}
# daily step:
Dist <- 50
ratioValue <- 1.02
Bias <- 0
startInd <- Dist
results <- NULL
results$Signal <- 0
for (k in seq((startInd+Bias+1),length(input[,1]),by=1)) {
print(as.Date(input[k,1]))
train <- input[(k-Dist):k,]
train <- Optimize(train,ratioValue)
ratio <- SignalPredictor(train,ratioValue)
results$Signal <- c(results$Signal,ratio)
}
Optimize <- function(inputData,ratioValue) {
L <- dim(inputData)[1]
mydist <- 1
mycheck <- -1
repeat {
mytest <- inputData[L,]
mytrain <- inputData[mydist:(L-1),]
probDown <- SurvivalProb(mytrain,"Down")
probUp <- SurvivalProb(mytrain,"Up")
ratio <- (probUp/probDown)-ratioValue
if ( (sign(ratio)*mytest$DailyRevenue >= 0) ) {mycheck <- 1}
if (mycheck == 1) {break}
if (mydist >= (L-10)) {
mycheck <- 1;mydist <- 2;break
}
mydist <- mydist + 1
}
mydist <- mydist - 1
inputData[mydist:L,]
}
Dist <- 50
ratioValue <- 1.02
Threshold <- 0
In the Fig. 2 the green parts correspond to the positive values of the ratio where the calculated probability for increasing $Close$ price is larger than for decreasing one. The red part shows the opposite behaviour.
The best signal buy/sell is generated when the ratio changes the sign:
from red to green : buy, from green to red: sell .
The black curve presents the $Close$ values, the blue line represents the values of $EMAV$.
By manipulating with the above parameters ($Dist$,$ratioValue$, $Threshold$ and $EMAV$) one can create different strategies. Using an initial capital equal to the $Close$ value at the initial date of the game, the total income generated by buy and sell signals for the above period and parameters is $16.47$ USD what corresponds to the $41.1$ % of profit from the considered period of time (2013-03-13 - 2016-06-17) .
Conclusions:
If you place capital into financial market it is always better to use several independent models for prediction of behaviour of financial instruments. If most of the methods are coming to the same conclusions, one can decide to take action: to sell or to buy the instrument(s).
The presented model could be treated as an additional source of such a knowledge. From technical point of view the script is easy to adopt to any financial data and has a lot of room for improvement. The most important part of the algorithm is the definition of censors ($censorUp$,$censorDown$) and "time to event" ($TimeToEventUp$,$TimeToEventDown$). I would appreciate any hints concerning improvement of the algorithm.
Hope, the note could be used as an introduction for survival analysis in a financial market. Comments (and links) are very welcome.
Thanks for reading !
Bogdan Lobodzinski
Data Analytics For All Consulting Service
[1] Guangliang Gao, Zhan Bu, Lingbo Liu, Jie Cao, Zhiang Wu: A survival analysis method for stock market prediction. BESC 2015: 116-122
Code for generation Fig. 2:
shift <- 47
factorSig <- 21
Sig <- sign(results$Signal)
L<-length(Sig)
Sigdf <- data.frame(x=input[(startInd+Bias):length(input[,1]),1],Sig=Sig*factorSig)
JustLine <- data.frame(xTime=input[(startInd+Bias):length(input[,1]),1],Line=0*c(1:L)+shift)
titleStr <- paste("Brent Oil Future: period from ",as.Date(input[(startInd+Bias+1),1]),
" to", as.Date(input[(length(input[,1])),1]))
ggplot(Sigdf, aes(x=as.Date(x), y=Sig+shift)) +
geom_line() +
geom_ribbon(aes(ymin=shift, ymax=ifelse(Sig+shift>shift,Sig+shift,shift)),
fill = "green", alpha = 0.5,colour = "green") +
geom_ribbon(aes(ymin=ifelse(Sig+shift < shift,Sig+shift,shift),ymax=shift),
fill = "red", alpha = 0.5,colour="red") +
geom_line(data = JustLine, aes(x=as.Date(xTime), y=Line)) +
geom_line(data = input[(startInd+Bias+1):length(input[,1]),],
aes(x=as.Date(input[(startInd+Bias+1):length(input[,1]),1]), y=Close)) +
geom_line(data = input[(startInd+Bias+1):length(input[,1]),],
aes(x=as.Date(input[(startInd+Bias+1):length(input[,1]),1]), y=EMAV, colour=4)) +
ggtitle(titleStr) +
labs(x="Date", y="Price in USD") +guides(colour=FALSE)
